Apakah Anda sedang mencari Struktur statis tertentu dan statis tak tentu, jika iya? maka Anda berada di website yang tepat.
Semoga artikel berikut ini dapat bermanfaat.
Pada dasarnya sifat sturktur dibagi menjadi dua yaitu Statis Tertentu dan Satatis Tak Tentu. Struktur statis tertentu dapat dianalisis dengan menggunakan persamaan statika atau kesetimbangan yaitu, ( Momen (∑M) = 0 ; Gaya Horizontal (∑H) = 0; Gaya Vertikal (∑V) = 0).
Sedangkan untuk analisis struktur statis tak tentu tidak bisa hanya diselesaikan dengan menggunakan prinsip statika atau kesetimbangan tersebut melainkan harus menggunakan bantuan persamaan lain berupa persamaan sudut penurunan dan persamaan penurunan (deflection).
Struktur Statis Tertentu
Struktur statis tertentu adalah struktur yang memiliki reaksi – reaksi tumpuan yang dapat ditemukan sedemikian rupa dengan tiga persamaan keseimbangan, Sifat dari struktur.
Ada beberapa contoh dari struktur yang termasuk ke dalam Struktur statis tertentu, yaitu :
1. Struktur Balok
Ada beberapa identifikasi balok yang termasuk ke dalam struktur statis tertentu diantaranya sebagai berikut :
Pada Gambar diatas adalah salah satu contoh struktur balok yang termasuk ke dalam struktur statis tertentu. Balok sederhana, balok menggantung, dan balok kantilever bisa ditentukan dengan persamaan ststis terntentu. Oleh karena itu, sebuah balok yang terletak diatas dua atau lebih penyangga atau tambahan tumpuan jepit pada ujung-ujungnya, maka bisa terdapat dua atau lebih reaksi dari luar yang harus ditentukan.
2. Struktur Kerangka Kaku
Untuk kerangka kaku, identifikasi strukutur statis tertentunya adalah sebagai berikut :
Suatu kerangka kaku akan termasuk ke dalam statis terntentu karena terdapat reaksi luar hanya tiga saja. Kenapa demikian, karena statika hanya memberikan tiga syarat keseimbangan untuk gaya sebidang.
3. Struktur Rangka Batang
Suatu rangka batang bisa disebut struktur statis terntenu karena stabil dan mempunyai jumlah gata yang tidak diketahui kurang dari tiga dan jumlah batang dalam rangka batang tersebut.
Diatas adalah penjelasan tentang Struktur statis tertentu dan bagaimana sebuah struktur bisa bersidat ke dalam struktur statis tertentu.
Struktur Statis tak Tertentu
Agar dapat menganalisa struktur statis tak tentu diperlukan syarat-syarat tambahan yang sama banyak dengan reaksi kelebihannya sebagai tambahan untuk statika, atau banyaknya syarat-syarat “tak statis” harus sama dengan derajat ketidaktentuannya.
Syarat-syarat tambahan tersebut pada umumnya dipenuhi oleh bentuk struktur yang terdeformasi
1. Struktur Balok Statis Tak Tentu
Jika sebuah balok terletak di atas lebih dari dua penyangga atau sebagai tambahan jepitan pada satu atau kedua ujungnya, maka akan terdapat lebih dari dua reaksi luar yang harus ditentukan.
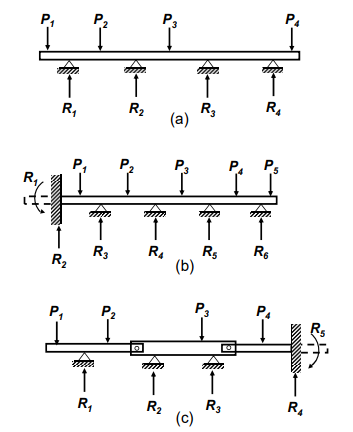
Statika hanya memberikan dua syarat keseimbangan untuk sistem gaya sejajar yang sebidang. Dengan demikian hanya dua reaksi yang dapat diperoleh, semua reaksi lainnya merupakan reaksi kelebihan dan tidak dapat ditentukan dengan hanya menggunakan persamaan statika.
Balok dengan reaksi kelebihan semacam ini disebut balok statis tak tentu. Derajat ketidaktentuannya ditentukan oleh jumlah rekasi kelebihan tersebut.
Jadi balok pada Gambar (a) merupakan struktur statis tak tentu berderajat dua karena jumlah reaksi yang tidak diketahui ada empat dan statika hanya bisa memenuhi dua persamaan keseimbangan, Sedangkan balok pada Gambar (b) merupakan struktur statis tak tentu berderajat empat, dan balok pada Gambar (c) bersifat statis tak tentu berderajat satu karena memiliki lima reaksi dan dua sendi dalam.
2. Struktur Kerangka Kaku Statis Tak Tentu
Jika suatu rangka-kaku bertingkat-satu memiliki reaksi luar lebih dari tiga, maka kerangka tersebut bersifat statis tak tentu, dan derajat ketidaktentuannya menjadi sama dengan jumlah reaksi kelebihannya.
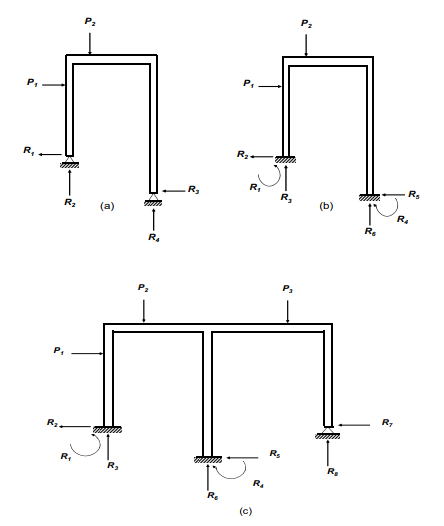
Dengan demikian, kerangka pada Gambar diatas merupakan struktur statis tak
tentu berderajat satu, berderajat tiga, dan berderajat lima.
3. Struktur Rangka Batang Statis Tak Tentu
Apabila suatu rangka batang memiliki sekurang-kurangnya tiga reaksi yang tak diketahui dan jumlah batangnya (m) lebih besar dari 2j- r, maka akan bersifat statis tak tentu, dengan derajat ketententuannya yakni menjadi : i = m – (2j – r).
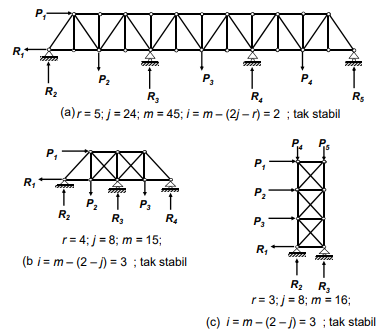
Rangka batang statis tak tentu pada Gambar (a) berderajat dua, karena mempunyai empat reaksi yang tak diketahui dan hanya ada dua persamaan keseimbangan. Gambar (b) dan Gambar (c) berderajat tiga, karena ada tiga batang kelebihan (m = 3j) ditambah tiga reaksi yang tidak diketahui, sedangkan persamaan keseimbangan yang ada hanya tiga saja.
Rangka batang umumnya terdiri dari serangkaian segitiga-segitiga yang
berhubungan satu sama lain seperti terlihat pada gambar di bawah:
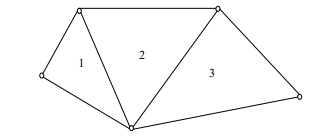
Dalam kasus ini segitiga pertama membutuhkan tiga buah titik hubung dan tiga buah
batang, Sedangkan setiap segitiga berikutnya membutuhkan dua batang tambahan, dan hanya satu titik hubung tambahan, sehingga: m – 3 = 2(j – 3) atau m = 2j – 3.
Baca juga : Bagian bagian jalan
Demikian yang dapat Teknik area bagikan, tentang Struktur statis tertentu dan statis tak tentu. Sekian dan terima kasih telah mengunjungi www.teknikarea.com, semoga bermanfaat dan sampai jumpa lagi di artikel Sipil berikutnya.